고정 헤더 영역
상세 컨텐츠
본문

- 평형상태에서 반도체의 전자, 정공 분포:

전도대의 전자 농도 분포 : n(E) = g(E)*f(E)

가전자대의 정공 농도 분포 : p(E) = g(E)*(1-f(E))

이며 단위는 [#/cm^3 * eV]이다.
- 반도체의 전자, 정공 농도를 구하기 위해 위의 식을 각각 적분하면,



전자의 농도는 위의 식과 같이 구할 수 있다.
정공의 농도는 위의 식과 같이 구할 수 있다.


Nc, Nv를 각각 전도대와 가전자대의 유효상대밀도함수라고 한다. 온도의 영향을 받는 반도체 재료의 고유특성이다.
- 평형상태 Intrinsic 반도체의 캐리어 농도 (ni, pi):

위 수식을 통해 intrinsic 반도체의 캐리어 농도가 아래와 같음을 알 수 있다.


Intrinsic 반도체의 페르미 에너지를 진성 페르미 에너지 (Efi)라 하고, 약 밴드갭의 중간에 위치한다. 정공과 전자의 유효질량이 다르면 Efi는 밴드갭의 중간에서 벗어난다. 유효질량이 가벼운 밴드쪽으로 Efi가 이동한다. 이는 유효질량이 가벼운 쪽이 상태밀도함수가 적고, 그에 따라 동일 캐리어농도를 위해 높은 확률로 전자가 채워지거나 비워져야하기 때문이다.
- Dopant와 Doping의 원리
1. n - type doping : 4족 원소인 Si로 이루어진 Si 결정에 5족 원소(P, As)를 치환불순물로써 도입한다. 5족 원소의 5개 가전자 중 4개는 실리콘 격자내 공유결합에 참여하고 나머지 1개 전자는 매우 불안정한 상태로 5족 원소 가전자 궤도에 존재한다. 작은 열에너지에 의해 5족 원소를 벗어나 전자가 이동이 가능하고 이에 따라 남은 5족 원소는 움직일 수 없는 (+) 이온 상태가 된다.
4족 원소인 Si로 이루어진 Si 결정에 5족 원소(P, As)를 치환불순물로써 도입한다. 전도대 바닥에 매우 가까운 donor 에너지상태인 Ed가 발생한다. 전자의 열에너지에 의해 손쉽게 donor에서 전도대로 전자 이동. 따라서 이동전자가 발생하고 전자를 잃은 donor 상태는 고정된 양(+)이온화.

2. p - type doping : 4족 원소인 Si로 이루어진 Si 결정에 3족 원소(B)를 치환불순물로써 도입한다. 3족 원소의 3개 가전자 모두 실리콘 격자 내 공유결합에 참여하고 나머지 한개의 격자 공유결합은 전자 1개가 모자란 매우 불안정한 상태이다. 작은 열에너지에 의해 주변 Si 결정의 가전자가 이동하여 정공이 발생한다. 남은 3족 우너소는 움직일 수 없는 (-) 이온 상태가 된다.
4족 원소인 Si로 이루어진 Si 결정에 3족 원소(B)를 치환불순물로써 도입한다. 가전자대 끝에 매우 가까운 acceptor 에너지상태가 발생한다. 전자의 열에너지에 의해 손쉽게 가전자대에서 acceptor로 전자가 이동하여 정공이 발생한다. 전자를 얻은 acceptor 상태는 고정된 음(-)이온화.

*donor : 이동전자를 발생시키는 불순물
*acceptor : 정공을 발생시키는 불순물
- 평형상태 Extrinsic 반도체의 캐리어 농도 (n0, p0)
이제, intrinsic 반도체에 doping을 해보자.

위 intrinsic 반도체의 농도를 이용하여 Extrinsic 반도체의 캐리어 농도를 다시 표현할 수 있다.

이와 같이 식을 유도할 수 있고 이 두 식을 다시 곱하면,
다음과 같은 결과를 얻을 수 있다.

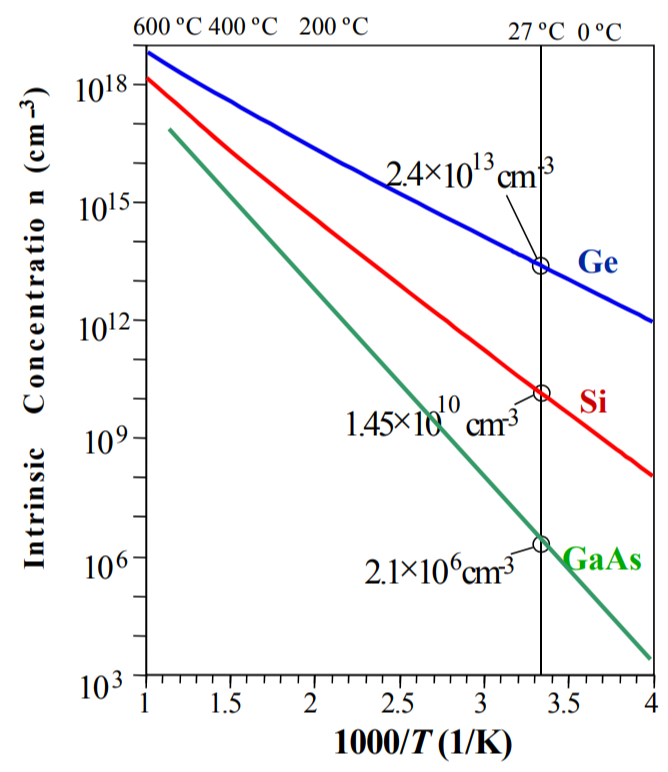
즉, 도핑에 무관하게 두 캐리어 농도의 곱은 항상 같고, 크기는 intrinsic 캐리어 농도의 제곱이다.
>> n0*p0=ni^2을 유지하며, 다수 캐리어가 소수 캐리어의 수를 억제하여 균형을 맞춘다.
(농도가 증가해도 n0와 p0가 만나서 recombination될 확률이 높아져 전자가 많으면 정공이 줄어드는 방식으로 균형이 맞춰진다.)
- 축퇴(degenerated) 반도체와 비축퇴(nongenerated) 반도체
1. 축퇴 반도체 : 일반적인 도핑 농도를 가진 반도체에 해당한다. 페르미 에너지가 밴드갭의 중간정도에 위치한다.
2. 비축퇴 반도체 : 아주 높은 도핑 농도를 가진 반도체에 해당한다. 페르미 에너지가 Ec또는 Ev에 매우 근접한다. 도핑 에너지 상태들이 서로 중첩하여 밴드를 형성하고 기본 밴드와 더해져서 반도체의 밴드가 넓어지고 밴드갭이 작아지는 현상이 발생한다. Ef가 Ec 또는 Ev 내부에 존재하며 매우 높은 전자 또는 정공 농도를 가진다.
- 완전 이온화와 동결
- 완전 이온화 : 도핑 원소의 이온화 에너지가 상온의 KT에 준하거나 작아서, 모든 도핑 원소가 이온화되어 캐리어를 발생하는 상태이다. 즉, 도핑농도 = Majority carrier 농도.
>> n doping : Nd = n0, p doping : Na = p0
- 동결 : T = 0K에서 전자의 열에너지가 0이므로, dopant들은 이온화 할 수 없음.
- 보상 (Compensated) 반도체 : n doping과 p doping이 서로 상쇄하여 보다 높은 doping 농도가 다수캐리어를 형성.
즉, Nd > Na 이면 n형 반도체이고 Na > Nd 이면 p형 반도체이고 Na = Nd 이면 intrinsic 반도체이다.

- 농도 근사




- 온도와 도핑 및 캐리어 농도의 관계
- 매우 저온에서는 KT<Ec - Ed, 즉 전자의 열에너지가 dopant의 이온화 에너지보다 작으므로 도핑효과 감소.
- 상온에서는 dopant가 완전 이온화되어, doping을 통해 extrinsic 반도체의 특성조절이 가능하다.
- 매우 고온에서는 intrinsic 캐리어 농도가 증가하여 doping 농도보다 높아지므로, doping에도 불구하고 intrinsic반도체의 특성을 가지게 된다.


- Extrinsic 반도체의 페르미 에너지 준위

- 높은 페르미 에너지는 높은 전자 캐리어 에너지를 의미한다. 페르미 에너지가 다른 두 재료가 접하면, 전자는 에너지가 낮은 재료로 이동하여 결국 페르미 에너지가 같아진다.


'반도체 > 소자' 카테고리의 다른 글
| 반도체 물성 및 소자 - 6. 반도체의 비평형상태 (0) | 2024.02.06 |
|---|---|
| 반도체 물성 및 소자 - 5. 캐리어 전송현상 (0) | 2024.02.06 |
| 반도체 물성 및 소자 - 3. 반도체의 이해 1 (0) | 2024.02.05 |
| 반도체 물성 및 소자 - 2. 기초 양자역학 (1) | 2024.02.05 |
| 반도체 물성 및 소자 - 1. 고체의 결정구조 (0) | 2024.02.05 |




