고정 헤더 영역
상세 컨텐츠
본문
- 에너지밴드의 형성 : 전자궤도가 중첩된 원자의 수만큼 에너지 준위가 분리되어야 하고, 무수히 많은 원자들이 인접하면 무수히 많은 중첩이 발생하여, 마치 연속된 에너지의 밴드를 형성한다.
최외각 전자부터 순차적으로 전자궤도 중첩이 발생하며 각각의 에너지 준위가 중첩에 의해 분리되어 에너지밴드를 형성한다. 기존 불연속 에너지준위 간의 에너지 간격으로 인해 에너지밴드간에 전자가 가지지 못하는 에너지 간격이 발생한다.
>> 허용(에너지)밴드와 금지(에너지)밴드로 나뉜다.

위 그림을 보면 3s, 3p가 만나 상호작용하여 결정거리인 a0에서 Ec, Ev, Eg가 형성된다.

Conduction band (전도대) : Ec위의 영역을 전도대라고 하며, 전자들이 원자간을 자유롭게 이동 가능하다.
Valance band (가전자대) : Ev아래의 영역을 가전자대라고 하며, 결정을 이루는 원자 간 결합에 기여하는 최외각 전자들이 가지는 에너지의 에너지밴드이다. 전자들이 결합에 묶여있다.
Energy bandgap (에너지밴드갭) : Eg를 의미하며 금지대의 에너지 폭이라고 할 수 있다.
- 캐리어의 발생: 전류가 발생하기 위해서는 캐리어가 필요하다.
- 0k보다 높은 온도에서는 모든 물질이 열에너지를 얻는다. 평균 열에너지는 밴드갭보다 크게 낮으나, 가전자대 전자중 일부가 열에너지 집중을 통해 전도대의 에너지를 얻고, 가전자대에는 빈 에너지상태(정공)가 발생한다. 이때 전도대의 전자는 원자사이를 이동가능한 캐리어이고, 전류가 발생가능하다. 전자가 정공을 만나면 전자와 정공이 재결합을 한다. 일정한 열에너지에 의해 생성과 재결합이 반복되고, 일정한 전자,정공 농도에서 균형을 이룬다.
- 금속, 절연층, 반도체의 구분

- 부도체 : 보통 매우 큰 밴드갭을 가지며, 상온에서 캐리어가 없다. 전압이 인가되어도 전류 발생이 없으며 캐리어 이동도도 매우 낮다.
- 반도체 : 보통 0.5eV < Eg < 3eV 의 값을 가진다. 상온에서 약간의 전자, 정공 캐리어가 발생하며 전압이 인가되면 전류가 발생한다. 캐리어의 이동도가 높다.
- 도체 : 밴드갭이 매우 작거나 없다. 매우 많은 전자 캐리어가 존재하며 매우 높은 전도도를 가진다.
- E-k diagram : 전자들이 공간에서 이동하는 방향에 따라 취할 수 있는 에너지가 다름.


- k (파수) 는 전자가 움직이는 방향이다.
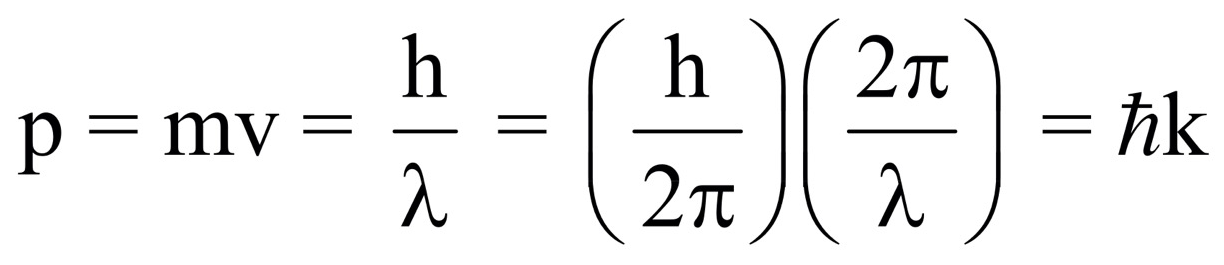


위의 식을 기반으로 그래프를 그리면,

위의 소자는 GaAs이며 Ec의 최솟값과 Ev의 최댓값의 k값이 같은 Direct bandgap을 가지고 있다. 이 경우 k의 변화없이 Recombination이 가능하다. 발광소자로 주로 이용된다.

위의 소자는 Si이며 Ec의 최솟값과 Ev의 최댓값의 k값이 다른 Indirect bandgap을 가지고 있다. 이경우 k의 변화가 있어야 Recombination이 가능하다.
>> GaAs가 Si보다 Ev에서 Ec로 전자가 이동할 때 필요한 운동량이 적다.
*유효질량 (Effective mass) : 양자역학적 결과를 고전역학으로 쉽게 계산하게 해주는 파라미터이다. 즉 결정내의 전자의 이동, 가속이 자유전자와 달라 뉴턴법칙이 성립하지 않고, 따라서 유효질량을 사용한다. 이 경우 뉴턴법칙이 성립한다.

유효질량은 이동도에 반비례하며 위의 식을 만족한다. 위 식을 통해 E-k diagram 에서 Ec의 최소점과 Ev의 최대점의 곡률에 반비례함을 알 수 있다. 따라서 위의 GaAs의 곡률이 Si보다 크므로 유효질량이 작다.
- 에너지상태밀도 (Density of States)와 페르미-디락 (Fermi-Dirac) 확률함수
1. Density of States (g(E)) : 에너지 밴드 내 전자가 차지할 수 있는 에너지 상태의 밀도로 단위 에너지, 단위 부피당 양자 상태수를 의미한다.



2. Fermi-Dirac (f(E)) : 결정에서 에너지 E의 양자상태에 전자가 채워질 확률이다.


파울리의 배타율을 만족하는 고체에서 바닥상태(ground state)란 0K에서 N개 입자(전자)가 밑바닥부터 채워진 상태를 말하며, 온도 변화에 따른 전자의 점유상태 변화는 페르미-디랙 분포함수 f(E)를 따른다. 페르미-디랙 함수란 임의의 온도 T의 열적평형 상태에서 에너지 준위 E가 전자에 의해 점유될 확률을 뜻하게 된다. 이때 페르미 레벨(Fermi level, Ef)은 반도체 내의 캐리어 거동을 설명하는 가상 준위를 뜻한다.
>>페르미 준위(Ef)의 정의
- 0K에서 전자가 가질 수 있는 최대 에너지 준위 (Ef 이하의 양자상태는 모두 전자로 채워지고, Ef 이상의 양자상태는 모두 비워진다.)
- 임의의 온도 T에서 전자가 채워질 확률 f(E=Ef)=1/2 인 에너지 준위
* 멕스웰 - 볼츠만 근사 : E-Ef >> KT인 경우 멕스웰 - 볼츠만 근사를 하여 간단한 식으로 근사할 수 있다.


'반도체 > 소자' 카테고리의 다른 글
| 반도체 물성 및 소자 - 6. 반도체의 비평형상태 (0) | 2024.02.06 |
|---|---|
| 반도체 물성 및 소자 - 5. 캐리어 전송현상 (0) | 2024.02.06 |
| 반도체 물성 및 소자 - 4. 반도체의 이해 2 (0) | 2024.02.05 |
| 반도체 물성 및 소자 - 2. 기초 양자역학 (1) | 2024.02.05 |
| 반도체 물성 및 소자 - 1. 고체의 결정구조 (0) | 2024.02.05 |




